Time-distributed controls

Section author: Simon W. Funke <simon@simula.no>

Background

Some time-dependent problems have control variables that are distributed over all (or some) time-levels. The following example demonstrates how this can be implemented in dolfin-adjoint.

One important aspect to consider is the regularisation term. For time-distributed controls, one typically uses wishes to enforce smoothness of the control variables in time. We will also discuss how such a regularisation term is implemented.

Problem definition

We consider the heat equation with a time-dependent source term \(f\), which will be our control variable:

\[\begin{split}\frac{\partial u}{\partial t} - \nu \nabla^{2} u= f(t) \quad & \textrm{in } \Omega \times (0, T), \\ u = 0 \quad & \textrm{for } \Omega \times \{0\} \\ u = 0 \quad & \textrm{for } \partial \Omega \times (0, T).\end{split}\]

where \(\Omega\) is the unit square, \(T\) is the final time, \(u\) is the unkown temperature variation, \(\nu\) is the thermal diffusivity, and \(g\) is the initial temperature.

The objective value, the model output of interest, is the norm of the temperature variable integrated over time, plus a regularisation term that enforces smoothness of the control in time:

\[J(u, f) := \int_0^T \int_\Omega (u-d)^2 \textrm{d} \Omega \text{d}t + \frac{\alpha}{2} \int_0^T \int_\Omega \dot f^2 \textrm{d} \Omega \text{d}t\]

The aim of this example is to solve the minimization problem \(\min_f J\) for some given data \(d\).

Implementation

We start by importing the needed FEniCS and dolfin-adjoint modules (note that fenics_adjoint is an alias for dolfin_adjoint):

from fenics import *
from fenics_adjoint import *
from collections import OrderedDict

Next, we define the expressions for observational data \(d\) and the viscosity \(\nu\).

data = Expression("16*x[0]*(x[0]-1)*x[1]*(x[1]-1)*sin(pi*t)", t=0, degree=4)
nu = Constant(1e-5)

Next, we define the discretization space:

mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, "CG", 1)

… and time:

dt = Constant(0.1)
T = 2

We are considering a time-distributed forcing as control. In the next step, we create one control function for each timestep in the model, and store all controls in a dictionary that maps timestep to control function:

ctrls = OrderedDict()
t = float(dt)
while t <= T:
    ctrls[t] = Function(V)
    t += float(dt)

The following function implements a heat equation solver in FEniCS, and constructs the first functional term.

def solve_heat(ctrls):
    u = TrialFunction(V)
    v = TestFunction(V)

    f = Function(V, name="source")
    u_0 = Function(V, name="solution")
    d = Function(V, name="data")

    F = ( (u - u_0)/dt*v + nu*inner(grad(u), grad(v)) - f*v)*dx
    a, L = lhs(F), rhs(F)
    bc = DirichletBC(V, 0, "on_boundary")

    t = float(dt)

    j = 0.5*float(dt)*assemble((u_0 - d)**2*dx)

    while t <= T:
        # Update source term from control array
        f.assign(ctrls[t])

        # Update data function
        data.t = t
        d.assign(interpolate(data, V))

        # Solve PDE
        solve(a == L, u_0, bc)

        # Implement a trapezoidal rule
        if t > T - float(dt):
           weight = 0.5
        else:
           weight = 1

        j += weight*float(dt)*assemble((u_0 - d)**2*dx)

        # Update time
        t += float(dt)

    return u_0, d, j

u, d, j = solve_heat(ctrls)

With this preparation steps, we are now ready to define the functional. First we discretise the regularisation term

\[\frac{\alpha}{2} \int_0^T \int_\Omega \dot f^2 \textrm{d} \Omega \text{d}t\]

Note, that \(f\) is a piecewise linear function in time over the time intervals \(K = [(0, \delta t), (\delta t, 2 \delta t), \dots, (T-\delta t, T)]\). Thus, we can write the integral as a sum over all intervals

\[\frac{\alpha}{2} \sum_{a_k, b_k \in K} \int_{a_k}^{b_k} \int_\Omega \dot f(t)^2 \textrm{d} \Omega\text{d}t\]

Discretising the time-derivative yields:

\[\begin{split}\frac{\alpha}{2} \sum_K \int_{a_k}^{b_k} \int_\Omega \left(\frac{f(b_k)- f(a_k)}{b_k-a_k}\right)^2\textrm{d}\Omega \\ = \frac{\alpha}{2} \sum_K (b_k-a_k)^{-1} \int_\Omega \left(f(b_k)- f(a_k)\right)^2\textrm{d}\Omega\end{split}\]

In code this is translates to:

alpha = Constant(1e-1)
regularisation = alpha/2*sum([1/dt*(fb-fa)**2*dx for fb, fa in
    zip(list(ctrls.values())[1:], list(ctrls.values())[:-1])])

We add the regularisation term to the first functional term and define define the controls:

J = j + assemble(regularisation)
m = [Control(c) for c in ctrls.values()]

Finally, we define the reduced functional and solve the optimisation problem:

rf = ReducedFunctional(J, m)
opt_ctrls = minimize(rf, options={"maxiter": 50})

from matplotlib import pyplot, rc
rc('text', usetex=True)
x = [c((0.5, 0.5)) for c in opt_ctrls]
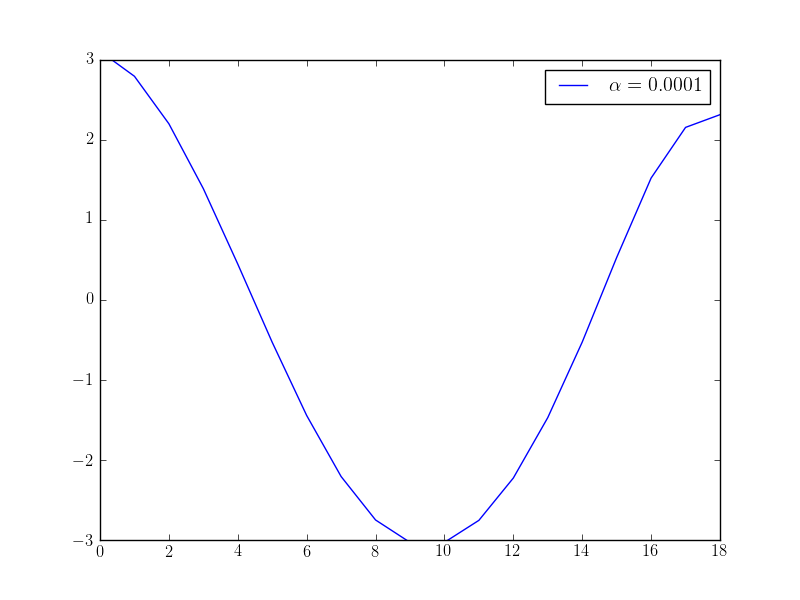
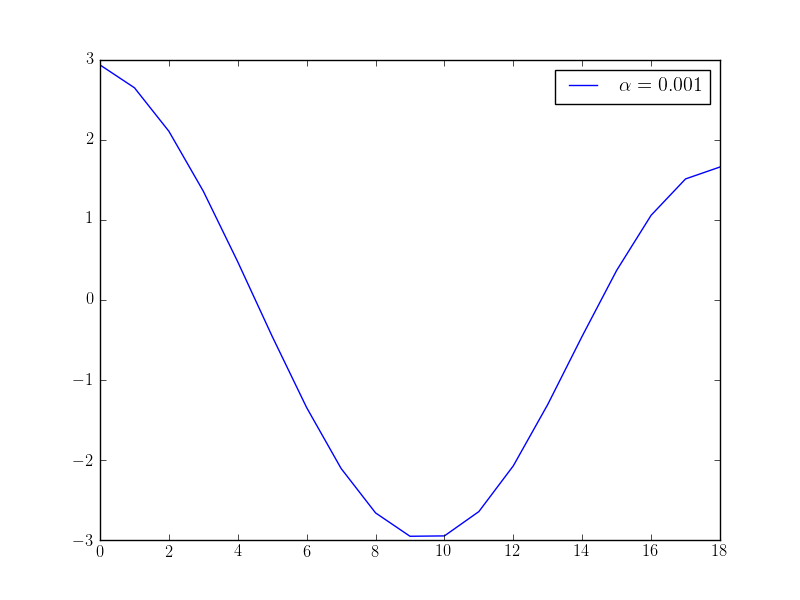
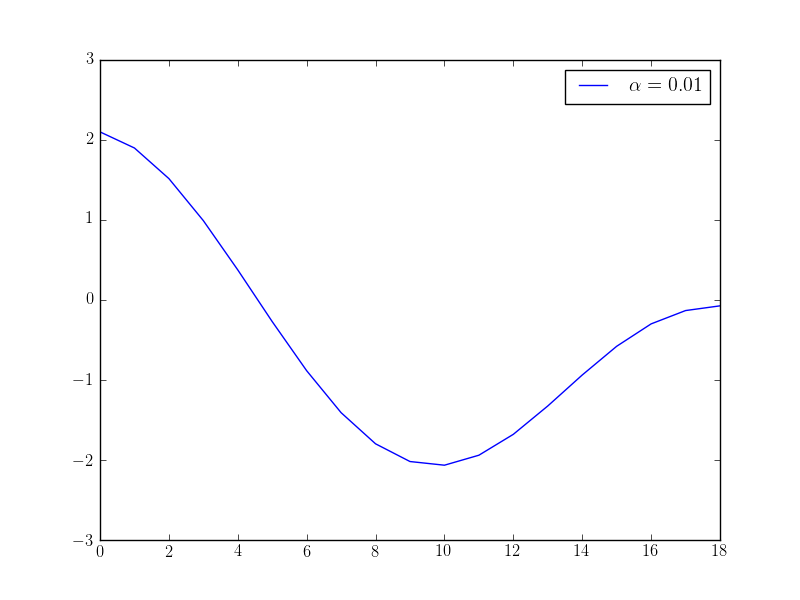
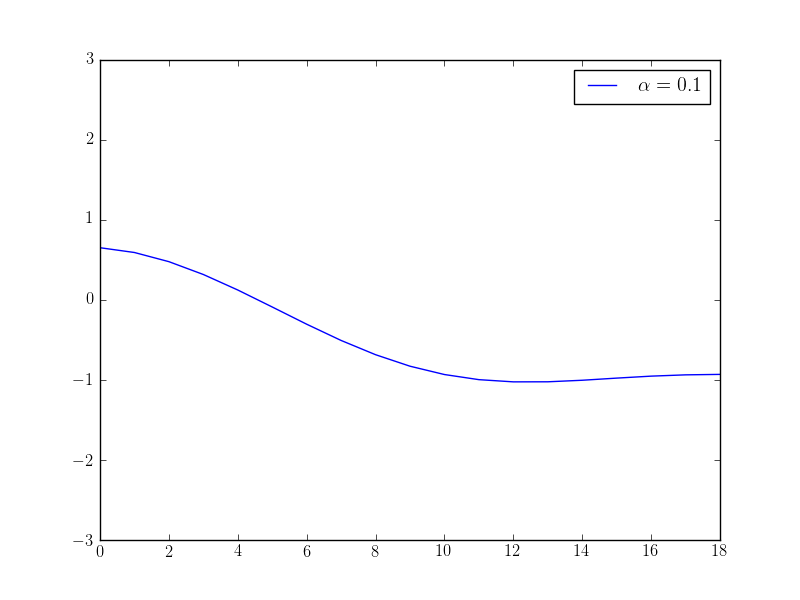
pyplot.plot(x, label="$\\alpha={}$".format(float(alpha)))
pyplot.ylim([-3, 3])
pyplot.legend()

If we solve this optimisation problem with varying \(\alpha\) parameters, we observe that we get different behaviour in the controls: the higher the alpha value, the “smoother” the control function becomes. The following plots show the optimised control evaluated at the middle point \((0.5, 0.5)\) over time for different \(\alpha\) values: